Lekce 4 - Obecná teorie a dělení fraktálů
V minulé lekci, Pojednání o chaosu, jsme mluvili o chaosu a atraktorech.
V této lekci si rozdělíme fraktály na L-systémy, IFS, polynomické a náhodné. Vysvětlíme si také obecnou teorii a pojmy soběpodobnosti a soběpříbuznosti.
Dělení fraktálů
Na základě generování fraktálů rozeznáváme některé jejich typy:
L-Systémy
L-systémy byly poprvé použity botanikem Aristidem Lindenmayerem (1968) pro simulaci vývoje mnohobuněčných organismů. Pro L-systémy se někdy používá označení fraktální křivky. Pravidla, sloužící ke generování fraktálu, nechť jsou nazvána parametry. Množina všech parametrů, nechť se nazývají abecedou příslušného L-systému. Jednotlivé parametry jsou označeny jedinečným symbolem. Počáteční symbol nebo množinu symbolů, který je základem pro generování fraktálních křivek se nazývá axiom (iniciátor). Ten představuje většinou velice jednoduchý nefraktální obrazec, např. trojúhelník, čtverec, přímka, krychle...
A nyní přikročíme ke konstrukci. Pravidlo, které jí popisuje (transformační pravidlo), se nazývá L-pravidlo či generátor. Toto pravidlo iterativně aplikujeme na všechny symboly, které jsou součástí iniciátoru. Každé stadium konstrukce fraktálu spočívá v přeměně každé předcházející linie v příslušnou kopii generátoru. Pro stádium konstrukce fraktálu před danou transformací se používá název předchůdce (predecessor) a pro stádium po dané transformaci se používá název nástupce (successor):
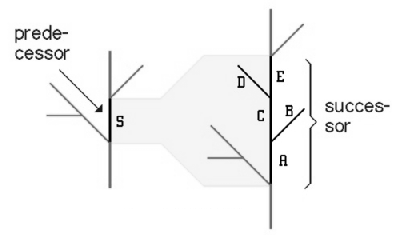
Postupem popsaným výše vzniká např. Kochova křivka. Samozřejmě že existuje více druhů L-systémů. Obecná klasifikace L-systémů nebyla dosud zavedena. Pokusy o ní stále vycházejí z konkrétních oborů, kde jsou L-sys. používány. Za nejpřesnější a nejobecnější metodu jejich třídění můžeme považovat rozdělení podle způsobu jejich generování (tedy klasifikace metod k tomu použitých). Nejhlavnější jsou parametrické L-systémy, kontextově senzitivní L-systémy (endogenní L-systémy) a environmentálně senzitivní L-systémy. L-systému jsou využívány v biologii, geologii a podobných přírodních vědách. Jejich plné využití zatím brání nedostatek údajů přesně popisujících morfologii přírodních objektů. To se projevuje zejména tehdy, když výzkum vedeme "do hloubky" a nestačí nám jen prosté zobrazení.
IFS
Existuje několik metod konstruování. První je stochastická cesta. Máme libovolný počáteční bod a na něj použijeme sadu transformačních pravidel. Jednotlivým pravidlům ovšem přiřadíme určitou pravděpodobnost, tzn. že příslušné pravidlo se vybírá náhodnou (stochastickou) cestou. Obecně si vyjádříme jednotlivá transformační pravidla jako funkce w1, w2,w3,…wn. Každé přiřadíme pravděpodobnost p1,p2…pn. Jejich součet dává 1 (100 %). Transformace mají afinní povahu. Tzn. že se skládají z násobné a přičítací matice.
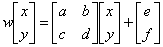
x, y -
souřadnice
Nový bod se stává opět počátkem pro další transformaci. Výsledky získáme po několika tisících iterací. Tuto chaotickou hru, jak se popsaný postup někdy nazývá, si ukážeme na příkladu Sierpinského trojúhelníku. Při jeho vytváření nám stačí zavést tři jednoduchá pravidla s třetinovou pravděpodobností:
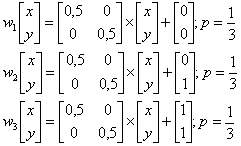
Zde vidíme vývoj několika prvních iterací a po 10000 iteracích.
Po několika prvních iteracích:
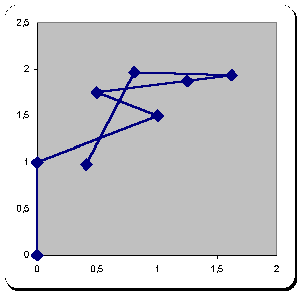
Po 10000 iteracích:
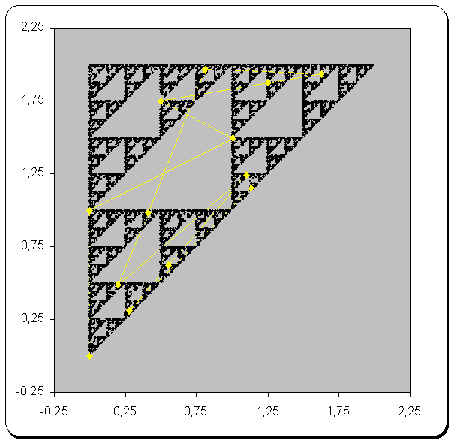
Další způsob je na představení mnohem jednodušší. Jedná se o prostě iterační metodu. Spočívá v tom, že máme nějaký základní obrazec (trojúhelník, čtverec…) a na něj aplikujeme nějaké geometrické pravidlo. Jako příklad vezměme opět Sierpinského trojúhelník. Nejprve tedy máme obecný, nejlépe ale rovno -stranný, -ramenný nebo pravoúhlý trojúhelník. Nyní označíme středy jeho stran a spojíme je úsečkou (narýsujeme střední příčky). Počáteční trojúhelník je rozdělen na 4 části a my prostřední vyjmeme. Získáme tři trojúhelníky (kopie toho původního) a na ně aplikujeme stejné pravidlo. Po dostatečném počtu iterací (nekonečném) dostaneme fraktální útvar. Metoda je triviální a je názornější, protože už od počátku vidíme obrysy cíle.
IFS fraktálů je samozřejmě mnoho, nejenom Sierpinského trojúhelník (Hausdorffova dimenze DH= log(3)/log(2)=1,585), jako další příklady lze uvést např.:
- Sierpinského kobereček(DH = log(8)/log(3) = 1,8928)
- Cantorovo diskontinuum(DH = log(2)/log(3) = 0,6309),
- Hilbertova křivka(DH = 2 docela dost na křivku, co)
- kapradí a spousta dalších.
Fraktálů typu IFS lze vytvořit velmi mnoho.
Polynomické fraktály
Na rozdíl od předešlých dvou typů je nelze většinou použít pro zkoumání přírodních objektů. Často ale vytvářejí fascinující obrazce, a proto jsou nejznámější. Vytvářejí se mapováním oblastí přitažlivosti pro různá řešení nelineárního systému. V soustavě souřadnic(často komplexních) testujeme různé hodnoty, které dosazujeme do původní rovnice. Na její výsledek aplikujeme iterativně stejné pravidlo. Pravou stranu dosadíme do levé a tak stále pokračujeme. Z toho vyplývá, že výsledku bychom se dobrali až v nekonečném čase. V praxi se tedy stanoví limitní hranice pro počet iterací. Pokud atraktor jasně směřuje do své oblasti přitažlivosti (to je ovšem u každého systému podle jeho autonomních pravidel), "výpočet" ukončíme a bod pro větší efektivitu obarvíme příslušnou barvou podle počtu iterací. Pokud dosáhneme limitní hodnoty, pak bod obarvíme implicitní barvou. Generování těchto fraktálů tedy není zcela exaktní, závisí na počtu iterací. Ovšem čím větší kvalitu požadujeme, tím větší nároky klademe na hardware počítače. Jejich výpočet je tedy časově velmi náročný proces, který podle současných znalostí nejde urychlit. Bez výpočtu nelze zjistit pro žádný bod v rovině (či 3D, 4D,…nD prostoru) zda patří, či ne do dané oblasti přitažlivosti. Mezi polynomické fraktály řadíme např. Mandelbrotovu množinu, Juliovy množiny a variace na ně. Rovnice, které je popisují, bývají až překvapivě jednoduché a tento typ fraktálů bude v tomto textu hojně diskutován.
Náhodné fraktály
Mezi náhodné fraktály rozhodně nepatří všechny ostatní. Je to ale velmi rozsáhlá a neuspořádaná skupina. Používá se hlavně pro zobrazování a modelování přírodních objektů a dějů. Některé vznikají velice jednoduše, např. náhodným přesouváním bodu, který zanechává za sebou stopu (Brownův pohyb). Jiné vykreslí hlávku zelí (salát je soběpříbuzný). Používají se tedy zejména pro popis přírodních objektů, neboť do výpočtu dávají prvek náhody. Náhodnými fraktály se na tomto webu budeme zabývat jen velice okrajově.
Obecná teorie
"Rozumné" eukleidovské tvary mají tu vlastnost, že se změnou měřítka nemění např. obvod. Takový čtverec si klidně zvětšujte až do aleluja, ale obvod, obsah a rozměry jednotlivých stran zůstanou nezměněny. Také těžko uvnitř čtverce uvidíte další, menší čtverce, či útvary jemu podobné. Čtverec je tedy tzv. geometricky hladký útvar. U fraktálů se setkáváme s naprostým opakem.
Vezměme např. problém měření délky ostrova, kterým se zabýval
Richardson. Nejprve ji změříme na mapě světa, třeba "odkrokujeme"
kružítkem. Získáme nějakou hodnotu x. Pak vezmeme mapu s
větším měřítkem a získáme hodnotu x+y. Poté pro změnu
obejdeme ostrov pěšky. Tak zachytíme ještě menší detaily, které na
mapách z pochopitelných důvodu zaneseny nejsou. Aby toho nebylo málo,
zmenšíme se do velikosti mravence a poctivě si to odpochodujeme (tedy
žádné přeskakování balvanů). Kdybychom se takto zmenšovali do
nekonečna, vyšla by nám délka ostrova nekonečná!
Podobný problém nenalézáme samozřejmě jen u délky pobřeží, např. Portugalsko uvádí délku hranic se Španělskem 1214 km, kdežto Španělsko má s Portugalskem hranici jen 987 km. Kterýkoli ostrov je tedy nekonečně členitý útvar. Richardson empiricky odvodil následující vztah:
K = N*eD
Kde jsou:
K– délka pobřežíN– počet úseček nutných k aproximacie– délka úsečkyD– konstanta, kterou neuměl Richardson odvodit, to dokázal až B. Mandelbrot
Další typické znaky fraktálů jsou lépe patrné na jiných modelech. Vezměme takový strom. Zdálky může vypadat jako trojúhelník, při přibližování (změně měřítka) se bude vyjasňovat jeho struktura (větve) při dalším přiblížení zjistíme, že jednotlivé větvičky "vytvářejí" obraz celého stromu. Tato vlastnost se nazývá soběpodobnost, ale s ní se setkáváme především u matematických modelů, v přírodě se objevuje hlavně soběpříbuznost.
Soběpodobnost
Kterákoliv část fraktálu je přesnou kopií původního motivu. Jak již bylo řečeno, jinde než u matematických struktur se s ní nesetkáme. Ty se naštěstí dají velice dobře znázornit, takže váš počítač může vykreslit i velice efektní soběpodobné útvary
Soběpříbuznost
Kterákoliv část fraktálu je podobná původnímu vzoru. V přírodě se
jedná např. o větve či kořeny stromu, mraky, pouštní duny atd. Z
problému zkoumání délky ostrova vyplývá jeden závažný důsledek. Pokud
totiž nabývá křivka nekonečné délky, měla by v rovině "zabírat o něco
více místa", než hladký útvar. To "více místa" se nazývá
Hausdorffova dimenze a u fraktálů je vždy větší
než topologická dimenze. Přímka má topologickou
dimenzi 1, čtverec 2, krychle
3, nadkrychle 4 atd. Jestliže obvod fraktálu K =
N*eD, pak měřítko s=1/N. Dosazením K=1 je
Hausdorffova dimenze DH= log(N) / log(1/s). V praxi nám většinou
nestačí takto jednoduše dosadit, používá se několik metod, např.
obvodová metoda nebo mřížková metoda.
V další lekci, Mandelbrotova a Juliova množina, probereme Mandelbrotovu a Juliovu množinu, jejich popis a uvedeme zdrojový kód ke generování těchto známých fraktálů.



