Dynamika
(pozn. jednotky v tabulkách na straně 103-104)
- zkoumá příčiny a podmínky pohybu, příčinou pohybu je vždy síla (=dynamis). Na rozdíl od kinematiky, která zkoumá samotný pohyb (jak se hýbe). Zakladateli dynamiky jsou Galelio, Huygens a Newton, který položil její základní zákony (platí pro makroskopická tělesa, pohybující se o mnoho menší rychlostí, než rychlostí světla C).
Síla
F [N]- síla nám popisuje vzájemné působení těles (interakci), vektorová veličina, určena velikostí, směrem a polohou svého působiště (obvykle v těžišti tělesa nebo hmotném bodě). Znázorňujeme orientovanou úsečkou:

Vzniká:
1) vzájemným dotykem (mechanická síla - přemístím rukou, míč o stěnu, náboj z pušky)
2) prostřednictvím silového pole (gravitační - planety, elektrická – nabitá tělesa, magnetická - magnety)
- síly jsou pojmenovány podle objektů, které na sebe působí, neexistuje sama o sobě, vždy vyvolána vzájemným působením hmotných objektů.
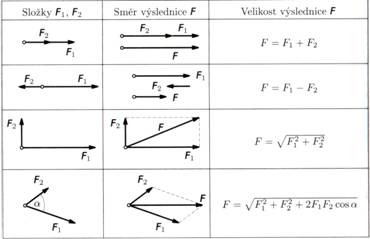
Vektorové skládání sil
- působí-li na těleso více sil najednou (složky), můžeme je nahradit jednou silou se stejným poh. účinkem (výslednice = vektorový součet složek - F = F1 + F2 + .... Fn).
účinky
- pohybové F--> O F
- deformační (změna tvaru nebo objemu) v
O
Tuhé těleso a hmotný bod
Hmotný bod
= smyšlený bodový objekt, který má hmotnost, ale nemá rozměry. Nahrazujeme jím těleso, pokud jeho rozměry jsou zanedbatelné vzhledem k uvažovaným vzdálenostem pohybu, hmotný bod se umísťuje do těžiště tělesa, má jeho hmotnost. Používáme ho pro zjednodušení.
Tuhé těleso - viz. otázka 4
Vztažná soustava –umístění HB v prostoru a čase, zavedené čtyři souřadnice: x, y, z, čas t.
Inerciální vztažná soustava - spojena se zemí, platí zde všechny Newtonovy zákony
Neinerciální vztažná soustava je taková soustava, která se vzhledem k inerciální vztažné soustavě pohybuje jinak než rovnoměrně přímočaře. Nejjednodušší je ta, která se vzhledem k inerciální vztažné soustavě pohybuje rovnoměrně zrychleným přímočarým pohybem a má konstantní zrychlení. (např. výtah), není spojena se zemí.
Neplatí zde 1. a 3. newtonův zákon.

Když se výtah nepohybuje: inerciální vztažná soustava (FG = m g)
Když se pohybuje se zrychlením a, působí na těleso kromě FG také setrvačná síla FS = -a m (v opačném směru než zrychlení)
F = FG + FS = mg +- a m
Při volném pádu (a = g) by byla výslednice F = 0 a těleso by bylo v beztížném stavu (výsadkář)
Newtonovy pohybové zákony
I. Zákon setrvačnosti
Těleso setrvává v klidu nebo rovnoměrném přímočarém pohybu, pokud není nuceno nějakou silou tento svůj pohybový stav změnit.
=Izolované těleso (izolovaný hmotný bod) - nepůsobí na něj žádné síly. V pozemských podmínkách neexistuje -> model izolovaného tělesa = výslednice sil působících na těleso je nulová (kulička na stole, výsadkář). V = konst., V = 0, a = 0.
II. Zákon síly
a = F / m [m * s-2, m / s2]
Zrychlení, které uděluje síla tělesu, je přímo úměrné síle nebo výslednici sil, které působí na těleso a nepřímo úměrné hmotnosti tělesa.
F = m a \ pohybová rovnice
Fg = m g …g = gravitační/tíhové zrychlení. Tíhová síla – složena s grav. síly a odstředivé (otáč. Země Fs)
m = F / a - dynamické měření hmotnosti, když nemůžeme vážit, setrvačná hmotnost
s = at² / 2 - rovnoměrně zrychlený pohyb
Síla o velikosti 1N uděluje tělesu o hmotnosti 1Kg zrychlení o velikosti 1m * s-2
Dvě tělesa na sebe působí vzájemně dvoumi stejně velkými silami s opačným směrem. Tyto síly současně vznikají a zanikají. Jednu nazýváme akce a druhou reakcfe. A + R nejsou v rovnováze a nevyruší se, protože každá působí na jiné těleso.
př. Dvě dívky jsou na kolečkových bruslích a drží opačné konce provazu. Jedna z nich zatáhne za provaz. Pohybovat se však nezačne jen druhá dívka, ale i ta, která za provaz zatáhla. Táhnoucí dívka vyvolala působením síly – akce, to že druhá síla – reakce bude působit na ni samotnou.
Hybnost
- je vektorová fyzikální veličina, definovaná jako součin hmotnosti a okamžité rychlosti hmotného bodu, popisuje pohybový stav tělesa.
p = m ×v [kg × m × s–1 (kilogram metr za sekundu)]
Vektor hybnosti má stejný směr jako vektor okamžité rychlosti. Hybnost charakterizuje pohybový stav tělesa.
Změna hybnosti a impuls síly
Podle definice zrychlení platí
![]() .
.
Po dosazení
![]() .
.
Změní-li se rychlost tělesa při konstantní hmotnosti, pak je změna hybnosti
![]() .
.
Druhý pohybový zákon lze vyjádřit
![]() .
.
Z tohoto vztahu lze vyjádřit
Dp = F×Dt.
Součin F×Dt síly a doby, kterou na těleso působila, je impuls síly. Její jednotkou je N × s (newton sekunda) a je to stejná jednotka jako jednotka hybnosti kilogram metr za sekundu.
Zákon zachování hybnosti: na začátku i na konci děje je celková hybnost stejná
Celková hybnost soustavy je dána vektorovým součtem hybností obou těles :
p = p1 + p2
Tělesa na sebe působí akcí a reakcí. F1 = –F2. Podle druhého pohybového zákona platí:
![]()
p1 – p01 = – (p2 – p02)
p01 + p02 = p1 + p2
V izolované soustavě platí vedle zákona zachování hybnosti ještě zákon zachování hmotnosti:
Celková hmotnost izolované soustav těles je konstantní.
Celkovou hmotností soustavy rozumíme součet hmotností všech těles, z nichž se soustava skládá.
Po srážce dvou pohybujících se těles se obě tělesa budou pohybovat rychlostí v, kterou určíme vztahy:
p = (m1 + m2) ×v = p1 + p2 = m1 ×v1 + m2 ×v2
![]()
Využití zákona zachování hybnosti
V moderním letectví a v kosmonautice se uplatňují reaktivní motory. Tryskami motoru unikají velkou rychlostí plyny vznikající při spalování pohonných látek. Podle zákona zachování hybnosti je raketa uvedena do pohybu opačným směrem. V elektrárnách se používají reaktivní turbíny. Zákon zachování hybnosti se také projevuje zpětným nárazem při střelbě ze střelných zbraní.
Tíha tělesa
G[N] = m g - síla, kterou působí těleso na podložku, pokud je těleso v klidu, má velikost síly gravitační.
Odporové síly
- působí proti směru pohybu
1) tření
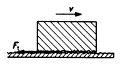 Při posouvání neboli smýkání tělesa po povrchu jiného
tělesa vzniká na styčné ploše obou těles třecí
síla Ft, která směřuje
vždy proti směru pohybu tělesa. Existence této síly znemožňuje
experimentální potvrzení zákona setrvačnosti. Její velikost nezávisí na obsahu styčných
ploch a při malých rychlostech na rychlosti tělesa, je přímo
úměrná velikosti kolmé tlakové síly
Fn a závisí na jakosti
styčných ploch.
Při posouvání neboli smýkání tělesa po povrchu jiného
tělesa vzniká na styčné ploše obou těles třecí
síla Ft, která směřuje
vždy proti směru pohybu tělesa. Existence této síly znemožňuje
experimentální potvrzení zákona setrvačnosti. Její velikost nezávisí na obsahu styčných
ploch a při malých rychlostech na rychlosti tělesa, je přímo
úměrná velikosti kolmé tlakové síly
Fn a závisí na jakosti
styčných ploch.
Ft = f × Fn
f je součinitel smykového tření (bej jednotky), jehož velikost je různá pro různé dvojice materiálů (tabulky str. 161). [f] = 1 Je-li těleso na podložce v klidu, pak na ně působí klidové tření. Součinitel klidového tření f0 je větší než součinitel smykového tření. (i jeho velikosti jsou v tabulkách str. 161). Velikost síly při klidovém tření: Ft = f0 × Fn. Tření využíváme každodenně například při chůzi. Jaké to může být, když je tření mnohem menší lze snadno zjistit, stačí k tomu náledí. Přílišné tření je ale na škodu, proto se ložiska a další součástky, které jsou v častém kontaktu a pohybu s jinými, mažou olejem.
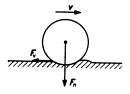 Valivý odpor
Valivý odpor
- vzniká vždy, když se po podložce valí těleso kruhového průřezu. Působením kolmé tlakové síly Fnse poněkud deformuje těleso i podložka. Deformace vyvolává odporovou sílu Fv, která působí na těleso a směřuje proti směru pohybu. Velikost odporové síly je přímo úměrná velikosti kolmé tlakové síly Fn, nepřímo úměrná poloměru R valícího se tělesa a závisí také na jakosti povrchu.
![]()
x (ksí) je rameno valivého odporu. (tabulky str. 161) [x] = m
Valivý odpor je mnohem menší než smykové tření, čehož se využívá v praxi – snažíme se maximálně využít kol pro pohyb nákladu i nás samotných.
Tření v praxi
1) snižování tření - lyže, snowboardy, olejování
2) zvyšování tření - při brzdění, posypy chodníků v zimě
Při rovnoměrném pohybu HB po kružnici má rychlost HB stálou velikost, ale mění se její směr. HB má dostředivé zrychlení ad. Podle zákona síly je příčinou zrychlení HB vždy síla, která má stejný směr jako zrychlení. Rovnoměrný pohyb po kružnici způsobuje dostředivá síla Fd.
![]()
Po ukončení působení dostředivé síly se HB pohybuje ve směru okamžité rychlosti, která se už nemění. Směr pohybu tedy je po tečně ke kružnici v bodě ukončení působení dostředivé síly. (točíme předmětem na provázku a provázek se přetrhne)
Pohybuje-li se soustava vzhledem k jiné po kružnici (např. auto v zatáčce vzhledem k zemi) pak tato soustava vzhledem k té druhé neinerciální – zemi považujme za soustavu v klidu a auto za neinerciální soustavu. Auto se pohybuje s dostředivým zrychlením ad vzhledem k zemi. Jako v každé neinerciální soustavě i zde působí setrvačná síla Fs. Působí opět proti zrychlení, které charakterizuje pohyb soustavy. Zde charakterizuje pohyb dostředivé zrychlení, proto setrvačná síla směřuje od středu – odstředivá síla. Tato síla nás vytláčí ven ze zatáčky, když jí projíždíme.
2) odpor prostředí - tření molekul plynu nebo kapaliny o povrch tělesa
Ft = F – rovnoměrný přímočarý pohyb
Ft > F – rovnoměrně zpomalený pohyb
Ft <
F - rovnoměrně zrychlený pohyb



 David se informační technologie naučil na
David se informační technologie naučil na