Mechanika a rovnovážná poloha tuhého tělesa
Mechanika tuhého tělesa
- část mechaniky, zabývající se pohyby tělesa, které nelze nahradit hmotným bodem (nelze zanedbat jeho rozměry a tvar a musí se uvažovat otáčivý pohyb tělesa)
Reálné těleso je nahrazeno tuhým tělesem, kvůli zanedbání deformačních sil.
Tuhé těleso je ideální těleso, jehož tvar ani objem se účinkem libovolně velkých sil nemění.
Pohyb tuhého tělesa se vždy skládá z pohybu posuvného (translace) a pohybu otáčivého (rotace).
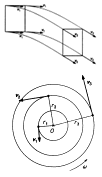 Posuvný pohyb -
všechny body tělesa opisují trajektorie stejného tvaru a v daném
okamžiku mají všechny body tělesa stejnou rychlost
v. (vagón jedoucí po přímé
trati)
Posuvný pohyb -
všechny body tělesa opisují trajektorie stejného tvaru a v daném
okamžiku mají všechny body tělesa stejnou rychlost
v. (vagón jedoucí po přímé
trati)
Otáčivý pohyb - všechny body mají v daném okamžiku stejnou úhlovou rychlost w. Nejjednodušší případ otáčivého pohybu je otáčení tuhého tělesa kolem nehybné osy (dveře, kolotoč, brusný kotouč).
Pohyb složený z těchto dvou pohybů koná valící se kolo, rotující disk nebo planety.
Moment síly
Chceme-li posoudit, jaký je otáčivý účinek síly na tuhé těleso, musíme zavést veličinu moment síly M (vektorová veličina). Závisí na velikosti síly.
Velikost momentu síly se určí ze vztahu
M = F × r × sin α (v tab není sin alfa, čili ten platí jen pro r kolmé k F)
[M] = N × m (newton metr) → tato jednotka má sice stejný rozměr jako práce a energie, ale moment síly je vektorová veličina
a.... úhel, který svírá síla F se vzdáleností r od osy otáčení
 Je-li vzdálenost r kolmá
k vektorové přímce síly F (získáme ji,
proložíme-li vektor síly přímkou), bude platit M = F × r. r (dříve
d, kdyby se to někde vyskytlo) je pak kolmá vzdálenost vektorové
přímky síly od osy otáčení a nazývá se rameno
síly.
Je-li vzdálenost r kolmá
k vektorové přímce síly F (získáme ji,
proložíme-li vektor síly přímkou), bude platit M = F × r. r (dříve
d, kdyby se to někde vyskytlo) je pak kolmá vzdálenost vektorové
přímky síly od osy otáčení a nazývá se rameno
síly.
Naproti tomu prochází-li vektorová přímka síly F osou
otáčení, síla nemá otáčivý účinek, těleso se pohybuje
posuvně.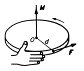
Vektor momentu síly leží v ose otáčení, orientace se určí pravidlem pravé ruky (pravotočivého šroubu).
Pokud těleso není upevněno, prochází osa otáčení těžištěm; v případě, že je těleso upevněno, prochází osa otáčení bodem, ve kterém je těleso upevněno.
- Působí-li na těleso více sil, jejich celkový otáčivý účinek je určen výsledným momentem sil
Výsledný moment sil M je vektorový součet momentů jednotlivých sil vzhledem k dané ose, tedy
M = M1 + M2 + … + Mn
Všechny momenty sil leží v ose otáčení, ale mohou mít různý směr. Ve zvláštním případě se otáčivé účinky sil navzájem ruší. Pak platí Momentová věta:
Otáčivé účinky sil působících na tuhé těleso otáčivé kolem nehybné osy se navzájem ruší, je-li vektorový součet momentů všech sil vzhledem k ose otáčení nulový:
M = M1 + M2 + … + Mn = 0
Podle momentů sil a momentové věty se skládají síly působící na tuhé těleso. Všechny síly, které působí na těleso, se skládají ve výslednici sil a pro skládání platí momentová věta.
F = F1 + F2 + … + Fn M1 + M2 + … + Mn = 0
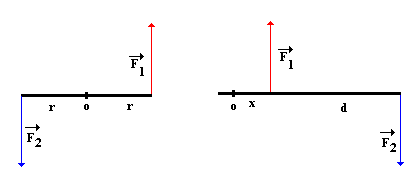
Skládají-li se dvě rovnoběžné síly stejné orientace, platí pro ně dvě rovnice:
F = F1 + F2 F1 × r1 = F2 × r2
První rovnice určí velikost výslednice, druhá polohu působiště.
Nejznámější příkladem pro skládání sil podle momentové věty je páka. Páka může být dvojzvratná nebo jednozvratná.
Na dvojzvratnou páku působí na jedné straně od osy otáčení tíha břemene a na druhé působíme silou. Abychom břemeno zvedli, musí být moment vyvolaný naší silou větší než moment vyvolaný tíhou břemene.
U jednozvratné páky je břemeno i působící síla na stejné straně od osy otáčení. Proto síla musí působit vzhůru.
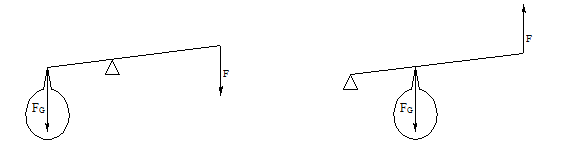
Další skládání sil - viz otázka 1. Dynamika
Dvojice sil
Pokud na těleso působí dvě stejně velké síly opačné orientace – F a F´, pak je nemůžeme nahradit jedinou silou. Tyto síly mají jen otáčivý účinek, který je vyjádřen momentem D dvojice sil. Rameno dvojice sil d je vzdálenost vektorových přímek obou sil.
Velikost momentu dvojice sil je rovna součinu velikosti jedné síly a ramene dvojice,
D = F × d (d = 2 r)
Moment D dvojice sil je kolmý k rovině, v níž leží síly, a jeho směr určíme pomocí pravidla pravé ruky.
Dvojice působí např. při utahování šroubu nebo při otáčení volantem, a to i když jím točíme jen jednou rukou – ruka spolu s volantem působí na čep volantu, který vyvolá reakci působící na volant. Dvojici pak tvoří síla, kterou působí ruka na volant, a reakce, kterou na volant působí čep.
Stejně jako se síly skládají, jedna síla se může rozložit na více sil. Při tom platí to, že kdybychom chtěli rozložené síly opět složit ve výslednici, budou opět platit obě rovnice, tj. skládání sil a momentová věta.
Těžiště tuhého tělesa
= působiště tíhové síly působící na těleso v homogenním tíhovém poli
určení: podpírání, zavěšování, výpočet
Je-li těleso zavěšeno, po ustálení lze určit těžnici – je to přímka, která spojuje těžiště tělesa a bod závěsu. Těžiště T pak je průsečíkem všech těžnic.
Pokud je těleso stejnorodé (homogenní = má všude stejnou hustotu) - střed, osa a rovina souměrnosti, na všech třech leží těžiště (ve středu souměrnosti)
Těžiště může být i mimo těleso (podkova, prstenec, dutá tělesa).
U nestejnorodých nebo geometricky nepravidelných těles se těžiště hledá experimentálně (zavěšením tělesa v takovém bodě, aby se ustálilo).
Rovnovážná poloha tuhého tělesa
Zavěšené nebo podepřené těleso je v rovnovážné poloze, jestliže svislá těžnice prochází bodem závěsu nebo podpěrným bodem a těleso je v klidu.
Podmínky rovnováhy:
Silová rovnováha – výslednice všech sil je nulová
F = F1 + F2 + … + Fn = 0
Momentová rovnováha – výsledný moment všech sil je nulový, tzn. platí momentová věta
M = M1 + M2 + … + Mn = 0
Tuhé těleso je v rovnovážné poloze, jestliže je vektorový součet všech sil, které na ně působí, i vektorový součet všech momentů těchto sil rovný nule.
Těleso může mít rovnovážnou polohu (znázorněno na kuličce a na zavěšeném kvádru):
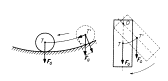 a) stálou (stabilní)
a) stálou (stabilní)
– po vychýlení z této polohy se do ní těleso opět vrací
– např. kulička v kulové misce, těleso otáčivé kolem osy nad těžištěm
– těžiště tělesa je v této poloze nejníže Þ nejnižší potenciální energie; vychýlení → zvýšení Ep
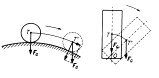 b) vratkou
(labilní)
b) vratkou
(labilní)
– po vychýlení z této polohy se do ní těleso už nevrací, snaží se zaujmout rovnovážnou polohu
stálou
– např. Sisyfův balvan – řecké báje – Sisyfos vytlačil balvan na kopec – nahoře poloha vratká, skutálel se na druhou stranu; těleso otáčivé kolem osy pod těžištěm
– v této poloze je těžiště tělesa nejvýše nad zemí Þ potenciální energie je nejvyšší; vychýlení → snížení Ep
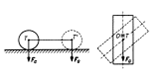 c) volnou
(indiferentní)
c) volnou
(indiferentní)
– po vychýlení z této polohy zůstává v nové poloze, je opět v rovnovážné poloze
– např. kulička na vodorovné podložce, těleso otáčivé kolem osy v těžišti
– výška těžiště se ani při vychýlení nemění Þ potenciální energie je konstantní; vychýlení → stejné Ep
Těleso podepřené na ploše je ve stále rovnovážné poloze, jestliže svislá těžnice prochází podstavou tělesa. (Na obrázku těžiště tělesa vystoupí do nové výšky h2)
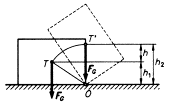 Stabilita tělesa je míra schopnosti
udržovat rovnovážnou polohu stálou. Je to práce,
kterou musíme vykonat, abychom těleso dostali z rovnovážné polohy stálé
do rovnovážné polohy vratké.
Stabilita tělesa je míra schopnosti
udržovat rovnovážnou polohu stálou. Je to práce,
kterou musíme vykonat, abychom těleso dostali z rovnovážné polohy stálé
do rovnovážné polohy vratké.
W = m × g × (h2 – h1) …g v tabulkách jako K
Stabilita je tím větší, čím níže je těžiště ve stálé rovnovážné poloze.
Kinetická energie tuhého tělesa
1) Při posuvném pohybu mají všechny body tělesa v daném okamžiku stejnou rychlost. Proto nemusíme kinetickou energii určovat jako součet kinetických energií všech bodů tělesa
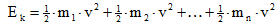 ,
,
ale můžeme ji vypočítat pro celou hmotnost tělesa
 ,
,
kde m = m1 + m2 + … + mn. Kinetická energie tělesa o hmotnosti m, které se pohybuje posuvným pohybem rychlostí v, je rovna kinetické energii hmotného bodu se stejnou hmotností a stejnou rychlostí.
2) Při otáčivém pohybu tuhého tělesa kolem nehybné osy opisují body tělesa kružnice, jejichž středy leží na ose otáčení. Úhlová rychlost ω je pro všechny body stejná, rychlosti jednotlivých bodů jsou přímo úměrné poloměrům kružnic, po nichž se pohybují =>
v1 = ω × r1, v2 = ω × r2, … vn = ω × rn.
Kinetickou energii tělesa určíme opět jako součet kinetických energií jednotlivých bodů
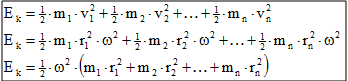
Při otáčení tuhého tělesa kolem nehybné osy závisí jeho kinetická energie na úhlové rychlosti otáčení; na hmotnostech jednotlivých bodů a na jejich vzdálenostech od osy otáčení => na rozložení látky v tuhém tělese.
moment setrvačnosti I = vyjadřuje rozložení látky tělesa vzhledem k ose. Vyplývá z hmotnosti a tvaru a charakterizuje schopnost tělesa udržovat otáčivý pohyb.
![]()
kde m1, m2, … mn jsou hmotnosti jednotlivých bodů, z nichž se těleso skládá a r1, r2, … rn jsou vzdálenosti bodů od osy.
[I] = kg × m2
Kinetická energie tuhého tělesa otáčejícího se kolem nehybné osy úhlovou rychlostí w je dána vztahem
kde J je moment setrvačnosti tělesa vzhledem k ose otáčení.
Moment setrvačnosti je pro různé tvary těles různý (zleva – obruč nebo dutý válec, plný válec, koule).

Největší moment setrvačnosti má těleso, které má hmotu soustředěnu co nejdál od osy - využití setrvačníky. Roztočené setrvačníky mají velkou kinetickou energii, osy setrvačníků s velkou úhlovou rychlostí udržují směr a na změnu jejich směru je potřeba velký moment síly. Setrvačníky se využívají u motorů, kde udržují rovnoměrný chod, udržování osy otáčení se využívá u umělých horizontů letadel.
Při otáčení tuhého tělesa působí jednotlivé body tělesa na osu setrvačnými silami.
volná osa - osa otáčení prochází těžištěm, setrvačné síly všech bodů se navzájem zruší a na osu nepůsobí žádná síla. Uchycení ve volné ose má nesmírný praktický význam. Kdyby například kola automobilů nebyla uchycena ve volné ose, jejich uchycení by bylo nesmírně namáháno a kolo by jednou uletělo. Proto se v pneuservisech vyvažují.
Koná-li těleso současně posuvný i otáčivý pohyb kolem osy procházející těžištěm tělesa, je jeho kinetická energie
![]()
kde m je hmotnost tělesa (umístěná v těžišti), v velikost rychlosti těžiště tělesa, J0 moment setrvačnosti vzhledem k ose otáčení jdoucí těžištěm tělesa, ω rychlost otáčení kolem této osy.



 David se informační technologie naučil na
David se informační technologie naučil na