Lekce 7 - IFS fraktály
V minulé lekci, IFS fraktály, jsme probrali Cantorovo mračno, Sierpinského trojúhelník, Sierpinského kobereček, Kapradí a Kochova vločka.
Euklidovská geometrie rozeznává jen několik základních těles (koule, kvádr, kužel atd.), tudíž je nemožné s její pomocí popsat tak složité útvary, jako hory, stromy, vodní hladinu, mraky a podobně. Tyto objekty lze však poměrně přesně popsat pomocí neuvěřitelně krátkých vzorců s využitím fraktální geometrie.
Fraktál je objekt, jehož geometrická struktura se opakuje v něm samém až do nekonečna. Nekonečno samozřejmě musíme v reálném světě omezit. Například stromy se větví na stále menší a menší větvičky, ale ty úplně nejmenší se už nevětví. Fraktály se obecně dělí na:
- Soběpodobné, se kterými se setkáme jen v matematických konstrukcích a kterýkoli výsek je přesnou kopií původního útvaru.
- Soběpříbuzné (jmenované stromy, mraky atd.), kde libovolný výsek je podobnou kopií původniho útvaru.
IFS
IFS (Interation Function System) je algoritmus, který stále opakuje tzv.
afinní transformace, dokud neproběhne zadaný počet iterací (počet,
kolikrát se geometrická struktura opakuje v mateřském útvaru). Fraktál je
tedy zadaný několika afinními transformacemi s těmito
parametry. Např. Sierpinského trojúhelník má 3 afinní transformace,
kapradina 4, strom 5 atd. Pokud budou všechny transformace používány
pravidelně, vznikne soběpodobný fraktál. Pokud budou používány každá s
jinou pravděpodobností (případný parametr p, kterým se zde
zabývat nebudu), algoritmus se nazývá hierarchický IFS (HIFS) a vznikne
fraktál soběpříbuzný. Afinní transformace s daným objektem provádí
následující operace: rotaci, zmenšování a posun. Vlastní popis afinní
transformace je dán vztahy:
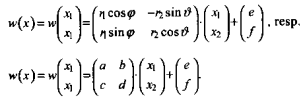
Vzorec na generování IFS fraktálů
Význam jednotlivých parametrů:
- Úhel fí: Otočení osy
x, v jejíž směru je útvar přeškálován parametremr1 - Úhel éta: Otočení osy
y, v jejíž směru je útvar přeškálován parametremr2 - e: Translace útvaru podle horizontální neotočené osy (horizontální posun celým útvarem)
- f: Translace útvaru podle vertikální neotočené osy (vertikální posun celým útvarem)
Zde jsou parametry (koeficienty) afinních transformací pro několik fraktálních útvarů:
Sierpinského trojúhelník
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.5 | 0 | 0 | 0.5 | 0 | 0 |
| 0.5 | 0 | 0 | 0.5 | 0.5 | 0 |
| 0.5 | 0 | 0 | 0.5 | 0.5 | 0.5 |

Vánoční stromeček
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0 | -0.5 | 0.5 | 0 | 0.5 | 0 |
| 0 | 0.5 | -0.5 | 0 | 0.5 | 0.5 |
| 0.5 | 0 | 0 | 0.5 | 0.25 | 0.5 |

Drak
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0 | 0.577 | -0.577 | 0 | 0.0951 | 0.5893 |
| 0 | 0.577 | -0.577 | 0 | 0.4413 | 0.7893 |
| 0 | 0.577 | -0.577 | 0 | 0.0952 | 0.9893 |

Labyrint
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.333 | 0 | 0 | 0.333 | 0.333 | 0.666 |
| 0 | 0.333 | 1 | 0 | 0.666 | 0 |
| 0 | -0.333 | 1 | 0 | 0.333 | 0 |

Větev
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.387 | 0.430 | 0.430 | -0.387 | 0.333 | 0. |
| 0.441 | -0.091 | -0.009 | -0.322 | 0.666 | 0 |
| -0.468 | 0.020 | -0.113 | 0.015 | 0.333 | 0 |

Sněhová vločka
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.255 | 0 | 0 | 0.255 | 0.3726 | 0.6714 |
| 0.255 | 0 | 0 | 0.255 | 0.1146 | 0.2232 |
| 0.255 | 0 | 0 | 0.255 | 0.6306 | 0.2232 |
| 0.370 | -0.642 | 0.642 | 0.370 | 0.6356 | -0.0061 |

Kapradina
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.849 | 0.037 | -0.037 | 0.849 | 0.075 | 0.1830 |
| 0.197 | -0.226 | 0.226 | 0.197 | 0.4 | 0.0490 |
| -0.150 | 0.283 | 0.260 | 0.237 | 0.575 | -0.084 |
| 0 | 0 | 0 | 0.16 | 0.5 | 0 |

Strom
| a | b | c | d | e | f |
|---|---|---|---|---|---|
| 0.849 | 0.037 | -0.037 | 0.849 | 0.075 | 0.1830 |
| 0.197 | -0.226 | 0.226 | 0.197 | 0.4 | 0.0490 |
| -0.150 | 0.283 | 0.260 | 0.237 | 0.575 | -0.084 |
| 0 | 0 | 0 | 0.16 | 0.5 | 0 |

Ve vztazích pro afinní transformace se provádí výpočty s maticemi. Konkrétně násobení matice o čtyřech a dvou prvcích a sčítání. Pro to platí následující obecný vzorec:
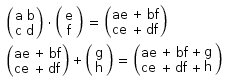
Zdrojový kód
Tak a to je prozatím vše. Doufám, že se mi alespoň trochu podařilo nastínit, o čem algoritmus IFS je a co že je to vlastně fraktální útvar. Aplikaci si odvodíte ze zdrojového kódu, je součástí programu IFSgen


 David se informační technologie naučil na
David se informační technologie naučil na