Lekce 5 - Mandelbrotova a Juliova množina

V minulé lekci, Obecná teorie a dělení fraktálů, jsme rozdělili fraktály na L-systémy, IFS, polynomické a náhodné. Vysvětlili jsme si také obecnou teorii a pojmy soběpodobnosti a soběpříbuznosti.

V této lekci probereme Mandelbrotovu a Juliovu množinu, jejich popis a uvedeme si zdrojový kód ke generování těchto známých fraktálů.

Mandelbrotova množina

Jedná se o polynomický nelineární deterministický fraktál a patrně nejznámější fraktál vůbec. Objevil jej Benoît Mandelbrot v 70. letech 20. století při pokusu o nalezení jakéhosi "katalogu" Juliových množin. Vzniká iterativně a je definován rovnicí z=z²+c, kde z i c jsou komplexní čísla. Je to potvrzení teorie, že i velice jednoduché systémy mohou vykazovat chaotické chování. V m-set, jak se zkráceně Mandelbrotova množina nazývá, je c konstanta a zároveň pozice vykreslovaného bodu. Počáteční hodnota z je [0;0] a slouží de facto k uchování hodnoty. Správně by se měly vyzkoušet všechny body roviny (dosadit je za c), ale pro |z| systém diverguje. Jak to můžeme tvrdit? Použijeme důkazu, který využívá trojúhelníkové nerovnosti pro komplexní čísla |a+b|>=|a|-|b|, kde za a dosadíme z² a za b konstantu c. Tedy |z²+ c| = |z²| - |c|. Nyní je nutné najít minimální hodnotu |z|, při jejímž překročení je |z²+ c|>|z|. Nazvěme tuto hodnotu třeba r. Potom r²-|c|=r a když převedeme vše nalevo, dostaneme r²-r-|c|=0. Z rovnice vyplývá, že r=(1+(1+4|c|^1­/2)/2. Známe tedy hodnotu r. Vzhledem k tomu, že před první iterací z=0, tak po ní z=c. V předchozích vzorcích můžeme tedy r nahradit |c|. |c|²-2|c|=0, tzn. |c|=2. Nyní můžeme bez obav vypustit z výpočtu všechny body, které nepatří do kružnice o poloměru 2 s počátkem v bodě [0,0]. Pro případ, kdy |z| směřuje k nule, neexistuje žádný důkaz, a proto musíme poctivě vyzkoušet všechny body v kruhu o poloměru 2. Všechny body vně a některé uvnitř, které divergují, nepatří do množiny, ostatní ano. M-set je souměrná podle osy x, podle osy y nikoli. Hranice mezi dvěma oblastmi přitažlivosti je nekonečně tenká, ale také nekonečně členitá. Její Hausdorffova dimenze je rovna 2, jedná se tedy o nejčlenitelnější útvar v ploše o omezeném obsahu. V základní množině nejsou pochopitelně patrné všechny detaily, a proto se provádí zoomování. Tak můžeme např. objevit menší kopie M-set, různě natočené či modifikované. M-set můžeme zvětšovat donekonečna a stále objevujeme nové a nové detaily. Jednotlivé body můžeme obarvit podle libovolné palety, a tak ze zdánlivě stejného obrázku dostaneme různé variace na to samé téma.

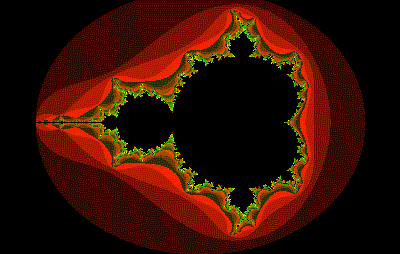
Mandelbrotova množina

Výpočet Mandelbrotovy množiny

Jedná se o Time escape algorithm. Potřebujeme dva vnořené cykly, které nám vyznačují zkoumaný čtverec (obdélník). V základní množině je to -2;2 a -2;2. Dále si určíme maximální počet iterací, např. 100. Při dobré implementaci dostáváme kvalitní obrázky i s přesností 30, ale čím menší přesnost, tím menší detaily. Řídící proměnné cyklů představují konstantu c, a proto uvnitř druhého cyklu se nachází další, jehož horní hranice je právě hodnota přesnosti. Pokud abs(z) > 2 tak se cyklus ukončí a bod se obarví příslušnou barvou. Pokud není nalezen směr atraktoru, bod do množiny patří a obarví se například černě. Díky paletě můžeme dosáhnou až překvapivě efektních obrázků. M-set nenaleznete v přírodě, ale třeba ve Photoshopu a podobných programech.

Algoritmus v metajazyce C

for (x=-2,x>2,x+=posun)
{
    a++
    for (y=-2,y>2,y+=pusun)
    {
        for (p=1,p>presnost,p++)
        {
            b++
            ztemp = [z]*[z]+[x,y]
            z = ztemp
            //Pokud (z1z1+z2z2) > 4 pak bod nepatří; obarvi bod [a,b]přislušnou barvou
        }
        //Pokud  cyklus proběhl celý, bod [a,b] patří
    }
}

Zde hranaté závorky neoznačují pole, ale komplexní číslo. Např. [z] se zde chápe jako [z1;z2]. Proměnná posun označuje jemnost našeho postupu. Pokud bude např. 0,1, cykly proběhnou 40x a obrázek bude mít rozměr 40x40 bodů. Výhodné je nastavit ji na 0,01, to je podle mě ideální kompromis mezi velikostí a rychlostí. Rychlost je skutečně limitující faktor, při přesnosti 100 a posunu 0,01 jsem napočítal přes 1 000 000 iterací. Tady už záleží jen na tom, jak si s příslušným jazykem dokážete pohrát. Na mém dinosauřím pentiu 200, 32 MB RAM trval výpočet základní množiny (posun = 0,01; přesnost 100) asi 3,5 vteřiny. Program byl napsán ve Visual Basic a optimalizován pro rychlost. Program i se zdrojákem si můžete stáhnout na http://www.sweb.cz/…et_balik.exe, v případě nefunkčnosti pod článkem. Rozhodně není dotažený do konce, a tak pokud máte VB, zkuste si své vývojářské schopnosti. Doporučuji při kompilaci zakázat všechny ochrany proti chybám. Sbírku algoritmů uvádím v několika jazycích zde.

Visual Basic

'Tady je zdroják ve Visual Basicu. Potřebuje jeden PictureBox, pár textboxů [6], a je dobré jej opatřit i tlačítkem start.
Private Declare Function SetPixelV Lib "gdi32" (ByVal hdc As Long, ByVal x As Long, ByVal y As Long, ByVal crColor As Long) As Long
Private Type Komplexni
x As Double
y As Double
End Type

Dim barva() 'počet barev-ten si musíte nastavit sami, ale měl by se rovnat či být větší než přesnost výpočtu
Dim hdc1 as long
Dim přesnost As Long, zx As Double
Dim zy As Double, i As Long
Dim t As Long, tt As Long
Dim ttt As Double, tttt As Double
Dim z As Komplexni, o As Double
Dim okolikT As Double, pres As Double
Dim pom As Long

hdc1 = picture1.hdc
Picture1.Cls 'Vyčištění pictureboxu-oceníte zejména tehdy, když je další obrázek podobný tomu předchozímu
startt = CDbl(Text1.Text) 'Uživatel nastaví x-ovou souřadnici
starttt = CDbl(Text2.Text) 'Uživatel nastaví y-ovou souřadnici
zoom = CDbl(Text3.Text) 'Uživatel nastaví zvětšení
přesnost = CDbl(Text4.Text) 'Uživatel nastaví max. počet iterací pro jeden bod
pres = (přesnost \ 2) - 1 'Menší fígl, vysvětlen dále
výška = CLng(Text6.Text) 'Uživatel nastaví výšku obrázku(počet bodů)
šířka = CLng(Text5.Text) 'Uživatel nastaví šířku obrázku
okolikT = 1 / zoom 'Posun reálné a imaginární složky
ttt = startt
tttt = starttt
NaplňBarvy() 'Pouze imaginární procedura pro určení barev
For t = 0 To výška
ttt = ttt + okolikT 'Posun reálné složky
For tt = 0 To šířka
tttt = tttt + okolikT 'Posun imaginární složky
z.x = ttt 'Místo z=0 rovnou přiřadíme z hodnotu c[ttt,tttt]-opatření pro snížení počtu operací
z.y = tttt
For i = 1 To pres
zx = z.x * z.x - z.y * z.y + ttt ' Jedna iterace
zy = 2 * z.x * z.y + tttt
z.x = (zx * zx - zy * zy) + ttt' Druhá iterace- proto si můžeme dovolit přesnost dělit dvěma, na přesnost to nemá vliv
z.y = 2 * zx * zy + tttt 'Pokud vám nejsou operace s komplexními čísly známy, musíte mi věřit.
If z.x * z.x + z.y * z.y > 4 Then GoTo oto 'Pokud je mimo, vykresli bod. z*z je použito proto, že z2 je výrazně pomalejší
Next i
GoTo otoo1 'Pokud patří, nic nekresli (bod má barvu pozadí). Dost to zrychluje
oto:
SetPixelV hdc1, t, tt, barva(i) 'Funkce API je asi o dva řády rychlejší než metoda line
otoo1: 'Pokud neholdujete nepodmíněným skokům, tak se moc nerozčilte
Next tt
tttt = starttt 'Nastavení pomocné proměnné pro z na správnou hodnotu
DoEvents
Next t

Java

Nekomentovaný zdrojový kód v jazyce Java. Staženo z http://honzour.kgb.cz/ (teď to přesměrovává na libimseti.cz ), nevím jestli funguje:

import java.awt.event.;
import java.awt.;
import java.applet.;
import java.awt.image.;

public class mandel extends Applet {
Image i;

Image MandelBrot(int x,int y){
    int i,j,iter;
    double im,re,zr,zi,pom;

    int[] p=new int[x*y];
    for (i=0; i<x; i++) {
        re=3*i;
        re=re/x-2.1;
        for (j=0; j<y; j++) {
            im=3*j; im=im/y-1.5;
            zr=0;
            zi=0;

            for (iter=0; iter <= 9;) {
                pom=(zrzr-zizi)+re;
                zi=(2zrzi)+im;
                zr=pom;
                if (zrzr+zizi >= 4) break;
                iter++;
            }
            p[i+j*x] = (255<<24)|((25*iter) << 16) | ((255-20*iter) << 8) | 100+10*iter;
        }
    }
    return createImage(new MemoryImageSource(x, y, p, 0, x));
}

public void init() {
   i = MandelBrot(400,400);
}

public void paint(Graphics g) {
   g.drawImage(i,0,0,java.awt.Color.black,this);
   }
}

Zajímavé útvary netvoří jen rovnice z=z²+c. Známe různé variace dané např. změnou exponentu či úpravou původního vzorce ( z=sin(z²)+c, z=cos(z²)+c). Ještě zajímavější fraktály vzniknou, jestliže mocníme exponentem komplexním, ne reálným. Pak totiž začnou vznikat čtyřrozměrné útvary. Pokud vyříznete část 4D prostoru 3D prostorem, pak můžete spatřit, co jste ještě neslyšeli.

Následující bajty tohoto souboru obsahují nejprve "normální" m-set, a pak její variace:

Jiná paleta m-set

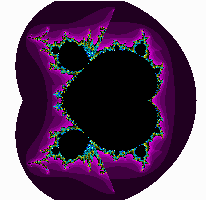
Malá modifikace vzorce

Ještě menší modifikace

Má oči po babičce

Polynomické fraktály tvoří fascinující obrazce a pokud máte dobrou tiskárnu, můžete si vytapetovat pokojíček.

Juliovy množiny

Jedná se o polynomický fraktál, stejně jako m-set. Podobnost zde nekončí. Jset (čeho to je asi zkratka?) vzniká na základě stejného vztahu jako M-set, tedy z=z²+c, kde z i c jsou komplexní čísla. Počáteční hodnota z ale není 0, ale rovná se pozici vykreslovaného bodu a c je libovolná konstanta, která se po dobu výpočtu celé množiny nemění. Na konci výpočtu obarvíme pochopitelně bod definovaný počáteční hodnotou z. Tím se od Mandelbrotovy množiny liší. Každá J-set vlastně představuje jeden bod v Mandelbrotově množině. M-set představuje jakýsi ucelený katalog všech Jset. Juliových množin je díky způsobu volby konstanty c nekonečný počet. Jejich historie je poněkud delší než historie m-set. Na průkopnické práce Gastona Julia a Pierre Fatoua ale pohlíželi tehdejší vědci s despektem a často je označovali jako matematické nestvůry. Uznání tedy došlo až později.

Hranice množiny je stejně jako u m-set fraktálem jehož Hausdorffova dimenze je rovna dvěma. Výsledný obrázek je silně závislý na konstantě c, takže pro jen nepatrně se lišící c můžete dostat i velice rozdílné výsledky (další příklad deterministického chaosu).

Jeden barevný příklad Juliovy množiny.

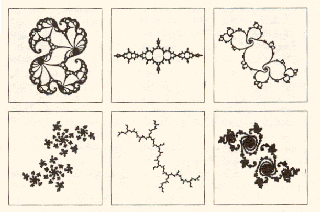
Celý soubor tentokrát černobílých obrázků.

Některé "zoomy" dokážou opravdu překvapit.

Pokud se v rovnici z=z²+c uspokojíte s reálným exponentem (2) a použijete komplexní, získáte útvar, pro jehož popis musíte zavést souřadnicový systém v hyperkomplexní rovině. Aby jste se mohli pokochat, musíte nejdříve vyříznout část 4D prostoru 3D prostorem. Pak už dokážete počítač přinutit vygenerovat obrázek. A že to za tu námahu stojí, potvrzuje následující obrázek.

Jset ve 4D

Tak tohle na ulici neuvidíte.

V další lekci, IFS fraktály, jsme probrali Cantorovo mračno, Sierpinského trojúhelník, Sierpinského kobereček, Kapradí a Kochova vločka.

Měl jsi s čímkoli problém? Stáhni si vzorovou aplikaci níže a porovnej ji se svým projektem, chybu tak snadno najdeš.